EP 7 of the ulab library series deals with the approx submodule used for approximation of numbers, function results or find the root of a function using bisect or newton method and trapz determination. In this article, we discuss the roles of each function and how to use them and sample programs as a guideline for further study and application.
approx
The approx submodule is a collection of estimation functions and finding the root of the data. The commands of this submodule are as follows.
- result = ulab.approx.bisect(func, a, b, xatol=2e-12, maxiter=100) It is used to find the root of a function of one variable using the Simple bisection method and two default values, and xatol and maxiter determine the exit.
- result = ulab.approx.fmin( func, x0, xatol=0.0001, fatol=0.0001, maxiter=None ) An approximation of a func written in the downhill simplex method, where x0 is the function’s default value and has three arguments to define the function’s stop condition. For example, if you want to run no more than 100 cycles, specify maxiter=100
- result = ulab.approx.interp( x, xp, fp ) Returns a linear approximation of a 1D array. The three arguments to this function have the following functions:
3.1 x is the row to be estimated.
3.2 xp is an array containing independent variables of the data.
3.3 fp is an array of numbers that are incremented by the same value. (monotonically increasing sequence of number)
In addition to all 3 arguments, there are left and right descriptors that act as values for the left and right members of the newly created array. The condition is that if x<xp[0], left is taken, and if x>xp[-1], right, but the left is usually equal to fp[0] or the first element of fp and the right is equal to fp[-1] or the last element of fp. - result = ulab.approx.newton( func, x0, stol=1.48e-08, rtol=0.0, maxiter=50) It is used to find the zero of a function given by the Newton Rafson method. (Newton-Raphson method or secant method or Halley’s method) with x0 as default and end work based on stol, rtol and maxiter values
- result = ulab.approx.trapz( y, x=None, dx=1.0, axis=1 ) To find values from 1 or 2 1D arrays, y and x, using the Trept-Zoidal method, if an independent variable x is assigned to a function, this value is used as a sample value relative to y.
Example Code 1
The example program code18-14 uses interp and trapz. The result is shown in Figure 1.
# code18-14 (approx)
import ulab as np
x = np.array([3.6, 7.9, 5.6, 8.4, 7.7, 9.2], dtype=np.float)
xp = np.array([4, 4.5, 5.5, 7.5, 10.5], dtype=np.float)
fp = np.array([1,2,4,7,11],dtype=np.float)
print(np.approx.interp(x,xp,fp))
print(np.approx.interp(x,xp,fp,left=0.4))
print(np.approx.interp(x,xp,fp,right=11))
print("trapz(x)=",np.approx.trapz(x))
Example Code 2
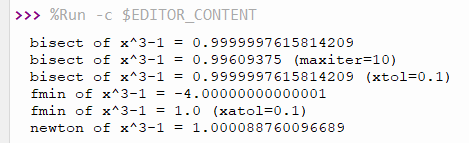
The code18-15 is to find the root of the function f with 3 methods and the result is as shown in Figure 2.
# code18-15 (approx)
import ulab as np
def f(x):
return x*x*x-1
print("bisect of x^3-1 = {}".format(np.approx.bisect(f,0,4)))
print("bisect of x^3-1 = {} (maxiter=10)".format(np.approx.bisect(f,0,4,maxiter=10)))
print("bisect of x^3-1 = {} (xtol=0.1)".format(np.approx.bisect(f,0,4),xtol=0.1))
print("fmin of x^3-1 = {}".format(np.approx.fmin(f,1.0)))
print("fmin of x^3-1 = {} (xatol=0.1)".format(np.approx.fmin(f,1.0,xatol=0.1)))
print("newton of x^3-1 = {}".format(np.approx.newton(f,3.0,tol=0.001,rtol=0.01)))
Conclusion
In this article, there are five commands for the approx submodule of ulab. The functions from numpy are interp and trapz, while the commands from the scipy library are newton, bisect, and fmin which have different functions. The value estimation has two important points: the variables used to estimate the values and the termination method which affect the outcome. The part of the termination method is there to prevent endless calculations.
The benefit of estimation is that when we have a model or equation of something, we can import the data to estimate the result, for example, there are 2 color spots, if we scale it up by 2 times what color will it be added? We have to find a color that is inserted and does not produce a square shape. Therefore, estimating the color of the spaces is a must.
Finally, have fun with programming.
Reference
(C) 2020, By Jarut Busarathid and Danai Jedsadathitikul
Updated 2021-08-21