[TH] ulab EP 4 linalg

บทความตอนที่ 4 ของไลบรารี ulab เป็นเรื่องของโมดูลย่อย linalg ที่ใช้สำหรับการคำนวณพีชคณิตเชิงเส้น ซึ่งถูกนำไปประยุกต์ใช้เพื่อแก้ปัญหาแบบเชิงเส้น และเป็นเครื่องมือในการทำนายหรือศึกษาลักษณะของสิ่งที่เกิดขึ้นแบบเชิงเส้น โดยในบทความนี้กล่าวถึงฟังก์ชันต่าง ๆ ของโมดูลย่อย linalg และตัวอย่างการใช้งานเบื้องต้น

linalg

โมดูลย่อย linalg เป็นการทำงานเกี่ยวกับพีชคณิตเชิงเส้นที่รองรับการคำนวณเพื่อหาค่าของ matrix inversion, dot product, determinant, eigenvalues, eigenvectors, Cholesky decomposition และ trace ซึ่งการใช้ฟังก์ชันต่าง ๆ เป็นดังต่อไปนี้

1. ผลลัพธ์ = ulab.linalg.cholesky( A ) ใช้ในการแก้สมการเชิงเส้น Ax = b ถ้าเมตริกซ์ A สมมาตร (symmetric square matrix) และเป็นบวกแน่นอน (positive definite matrix) นิยมใช้สำหรับหาค่ากำลังสองที่น้อยที่สุดเชิงเส้น (linear least square) สมการเชิงอนุพันธ์ย่อย (Partial differential equation) นำไปใช้ในเรื่องของวิธีมอนติคาร์โล (Monte Carlo method) และเป็นเครื่องมือหนึ่งในการศึกษาเรื่องการเงิน แต่ถ้าเมตริกซ์ A ไม่ใช่เมตริกซ์สี่เหลี่ยม (สมมาตร) และเป็นบวกแน่นอนจะทำให้เกิดความผิดพลาดในการทำงาน
2. ผลลัพธ์ = ulab.linalg.det( M ) หาค่าดีเทอร์มิแนนต์ (Determinant) ของเมตริกซ์ M
3. ผลลัพธ์ = ulab.linalg.dot( M, N ) ทำการคำนวณผลคูณจุด (Dot Product) ระหว่างเมตริกซ์ M และ N
4. eigenvalues,eigenvectors = ulab.linalg.eig( M ) คำนวณหาค่า Eigenvalues และ Eigenvectors ของเมตริกซ์สี่เหลี่ยม (ถ้าไม่ใช่จะเกิดความผิดพลาด)
5. ผลลัพธ์ = ulab.linalg.inv( M ) หาส่วนกลับหรืออินเวิร์สของเมตริกซ์สี่เหลี่ยม (square matrix) ถ้าเกิดข้อผิดพลาดสามารถหารายละเอียดความผิดพลาดจาก ValueError และที่ต้องระวัง คือ การคำนวณเพื่อหาส่วนกลับของเมตริกซ์นั้นมีความจำเป็นที่ต้องใช้หน่วยความจำจำนวนมากเพื่อเก็บเมตริกซ์ประเภท float ในการคำนวณผลลัพธ์
6. ผลลัพธ์ = ulab.linalg.norm( M ) ใช้สำหรับหาค่ารากที่สองของผลรวมกำลังสองของสมาชิกภายในแถวลำดับ
7. ผลลัพธ์ = ulab.linalg.size( n ) คืนค่าขนาดตามเงื่อนไขของ n คือ
   n = 0 คืนค่าจำนวนสมาชิก (elements) ในแถวลำดับ
   n = 1 คืนค่าจำนวนแถว
   n = 2 คืนค่าจำนวนสดมภ์ (column)
8. ผลลัพธ์ = ulab.linalg.trace( M ) หาผลรวมของสมาชิกในแนวทะแยงมุมของเมตริกซ์สี่เหลี่ยม

ตัวอย่าง 1

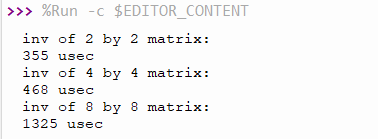
ตัวอย่างโปรแกรม code18-8 เป็นการคำนวณหาส่วนกลับเมตริกซ์ขนาด 2×2 4×4 และ 8×8 โดยผลลัพธ์ของการทำงานเป็นดังภาพที่ 1 ซึ่งจะพบว่า ขนาดของเมตริกซ์ยิ่งใหญ่ขึ้นยิ่งต้องใช้เวลาในการคำนวณมากขึ้นตามกันไป

#code18-8
import ulab as np
import time

print('inv of 2 by 2 matrix:')
m = np.array([[2, 1], [3, 5]])
t0 = time.ticks_us()
np.linalg.inv(m)
print("{} usec".format(time.ticks_us()-t0))

print('inv of 4 by 4 matrix:')
m = np.array([[7, 2, 1, 4], [5, 5, 4, 4], [0, 2, 8, 3], [8, 0, 3, 1]])
t0 = time.ticks_us()
np.linalg.inv(m)
print("{} usec".format(time.ticks_us()-t0))

print('inv of 8 by 8 matrix:')
m = np.array([[ 1, 2, 3, 4, 5, 6, 7, 8],
              [ 9,10,11,12,13,14,15,16],
              [21,18,19, 0,21,22, 0,10],
              [33, 0, 1, 0,29, 0,31,10],
              [49,34,35,36,37,38,39,10],
              [ 1, 1, 0,44,45, 0,47,10],
              [49, 0,51,52,53,54, 0,10],
              [ 1,58,59, 0,61, 0,63,10]])
t0 = time.ticks_us()
np.linalg.inv(m)
print("{} usec".format(time.ticks_us()-t0))

สรุป

จากบทความนี้จะพบว่า หน้าที่ของโมดูลย่อย linalg เป็นการคำนวณของเมตริกซ์เพื่อแก้ปัญหาทางพีชคณิตเชิงเส้น ซึ่งส่วนใหญ่มีเงื่อนไขการใช้งานที่ต้องระมัดระวังเนื่องจาก การใช้เมตริกซ์ที่ผิดเงื่อนไขในการทำงานจะส่งผลให้โปรแกรมเกิดความผิดพลาดในการทำงาน ดังนั้น การเขียนโค้ดคำสั่งจึงควรดักข้อผิดพลาดดังรูปแบบต่อไปนี้เพื่อรายงานประเภทความผิดพลาดที่เกิดขึ้น

try:
ชุดคำสั่ง
except ValueError as e
print(“{}”.format(e))

หรือ

try:
ชุดคำสั่ง
except IndexError as e:
print(“{}”.format(e))

สุดท้ายนี้ขอให้สนุกกับการเขียนโปรแกรมครับ

เอกสารอ้างอิง

1. การแยกแบบโซเลสกี้

(C) 2020, โดย อ.ดนัย เจษฎาฐิติกุล/อ.จารุต บุศราทิจ
ปรับปรุงเมื่อ 2020-11-10
ปรับปรุงเมื่อ 2021-08-12