[TH] ulab EP 7 approx

บทความตอนที่ 7 ของชุดไลบรารี ulab เป็นเรื่องของโมดูลย่อย approx ที่ใช้สำหรับการประมาณค่าของตัวเลข ผลลัพธ์ของฟังก์ชัน หรือหารากของฟังก์ชันด้วยวิธี bisect หรือ newton และการหาค่าด้วย trapz โดยในนบทความนี้กล่าวถึงบทบาทหน้าที่ของแต่ละฟังก์ชันพร้อมวิธีการใช้งาน และตัวอย่างโปรแกรมเพื่อเป็นแนวทางสำหรับการศึกษาการใช้งานและประยุกต์ใช้ต่อไป

approx

โมดูลย่อย approx เป็นที่รวมของฟังก์ชันทางด้านการประมาณค่า (approximating numerical data) และหาค่าราก (root) ของข้อมูล ซึ่งคำสั่งของโมดูลย่อยนี้มีรูปแบบการใช้งานดังต่อไปนี้

1. ผลลัพธ์ = ulab.approx.bisect(func, a, b, xatol=2e-12, maxiter=100) ใช้สำหรับหารากของฟังก์ชัน 1 ตัวแปร โดยใช้วิธีซิมเปิ้ลไบเซ็กชัน (Simple bisection method) โดยกำหนด func ที่เรียกใช้งาน และค่าเริ่มต้น 2 ค่า และมี xatol กับ maxiter เป็นตัวกำหนดการจบการทำงาน
2. ผลลัพธ์ = ulab.approx.fmin( func, x0, xatol=0.0001, fatol=0.0001, maxiter=None ) เป็นการประมาณค่าของ func ที่เขียนขึ้นด้วยวิธีการดาวน์ฮิลล์ซิมเพล็กซ์ (downhill simplex method) โดย x0 คือ ค่าเริ่มต้นของฟังก์ชัน และมี 3 อาร์กิวเมนต์ที่ใช้กำหนดเงื่อไขการหยุดทำงานของฟังก์ชัน เช่นต้องการให้ทำงานไม่เกิน 100 รอบ ให้กำหนด maxiter=100
3. ผลลัพธ์ = ulab.approx.interp( x, xp, fp ) คืนค่าการประมาณค่าแบบเชิงเส้นของแถวลำดับ 1 มิติ ซึ่งอาร์กิวเมนต์ทั้ง 3 ของฟังก์ชันนี้มีหน้าที่ดังต่อไปนี้
   3.1 x คือ แถวลำดับที่ต้องการนำมาประมาณค่า
   3.2 xp คือ แถวลำดับเก็บตัวแปรอิสระของข้อมูล
   3.3 fp คือ แถวลำดับของตัวเลขที่มีการเพิ่มขึ้นด้วยค่าที่เท่ากัน (monotonically increasing sequence of number)
   นอกจากทั้ง 3 อาร์กิวเมนต์แล้วยังมีตัวกำหนด left และ right ที่ทำหน้าที่เป็นค่าสำหรับสมาชิกทางซ้ายและทางขวาของแถวลำดับใหม่ที่สร้างขึ้น ตามเงื่อนไขคือ ถ้า x<xp[0] จะนำค่า left มาใช้ และ ถ้า x>xp[-1] จะนำค่า right มาใช้ แต่โดยปกติค่า left จะเท่ากับ fp[0] หรือสมาชิกตัวแรกของ fp และค่า right จะเท่ากับ fp[-1] หรือสมาชิกตัวสุดท้ายของ fp
4. ผลลัพธ์ = ulab.approx.newton( func, x0, stol=1.48e-08, rtol=0.0, maxiter=50) ใช้หาค่าศูนย์ของฟังก์ชันที่กำหนดด้วยวิธีนิวตันราฟสัน (Newton-Raphson method หรือ secant method หรือ Halley’s method) โดยกำหนด x0 เป็นค่าเริ่มต้นทำงาน และสิ้นสุดการทำงานโดยพิจารณาจากค่า stol, rtol และ maxiter
5. ผลลัพธ์ = ulab.approx.trapz( y, x=None, dx=1.0, axis=1 ) สำหรับหาค่าจากแถวลำดับ 1 มิติ จำนวน 1 หรือ 2 ตัว คือ y และ x โดยใช้วิธีเทรพ-โซอิดัล (Trape-zoidal method) ซึ่งถ้ามีการกำหนดตัวแปริสระ x แก่ฟังก์ชัน ค่านี้จะถูกนำมาใช้เป็นค่าตัวอย่างที่จะสัมพันธ์กับ y

ตัวอย่างโปรแกรม 1

ตัวอย่างโปรแกรม code18-14 เป็นการใช้ interp และ trapz และตัวอย่างของผลลัพธ์เป็นดังภาพที่ 1

# code18-14 (approx)
import ulab as np

x = np.array([3.6, 7.9, 5.6, 8.4, 7.7, 9.2], dtype=np.float)
xp = np.array([4, 4.5, 5.5, 7.5, 10.5], dtype=np.float)
fp = np.array([1,2,4,7,11],dtype=np.float)
print(np.approx.interp(x,xp,fp))
print(np.approx.interp(x,xp,fp,left=0.4))
print(np.approx.interp(x,xp,fp,right=11))
print("trapz(x)=",np.approx.trapz(x))

ตัวอย่างโปรแกรม 2

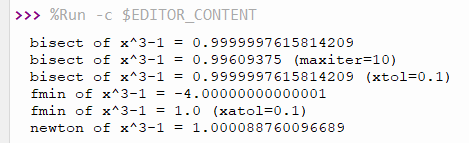
ตัวอย่างโปรแกรม code18-15 เป็นการหารากของฟังก์ชัน f ด้วย 3 วิธี และผลลัพธ์ที่ได้เป็นดังภาพที่ 2

# code18-15 (approx)
import ulab as np

def f(x):
    return x*x*x-1

print("bisect of x^3-1 = {}".format(np.approx.bisect(f,0,4)))
print("bisect of x^3-1 = {} (maxiter=10)".format(np.approx.bisect(f,0,4,maxiter=10)))
print("bisect of x^3-1 = {} (xtol=0.1)".format(np.approx.bisect(f,0,4),xtol=0.1))
print("fmin of x^3-1 = {}".format(np.approx.fmin(f,1.0)))
print("fmin of x^3-1 = {} (xatol=0.1)".format(np.approx.fmin(f,1.0,xatol=0.1)))
print("newton of x^3-1 = {}".format(np.approx.newton(f,3.0,tol=0.001,rtol=0.01)))

สรุป

จากบทความตอนนี้จะพบว่าชุดคำสั่งสำหรับโมดูลย่อย approx ของ ulab มีด้วยกัน 5 คำสั่ง โดย ฟังก์ชันที่นำมาจาก numpy ได้แก่ interp และ trapz ส่วนคำสั่งการทำงานที่นำมาจากไลบรารี scipy คือ newton, bisect และ fmin ซึ่งมีหน้าที่การทำงานที่แตกต่างกัน โดยการประมาณค่านั้นจุดสำคัญมี 2 สิ่ง คือ ตัวแปรที่นำมาใช้ประมาณค่า และวิธีการสิ้นสุดการทำงาน ซึ่งมีผลต่อผลลัพธ์ที่เกิดขึ้น และส่วนของวิธีการสิ้นสุดการทำงานมีไว้เพื่อป้องกันการเกิดการคำนวณไม่รู้จบ

ประโยชน์ของการประมาณค่า คือ เมื่อเรามีโมเดลหรือสมการของสิ่งใดสิ่งหนึ่งเราสามารถนำเข้าข้อมูลเพื่อประมาณค่าผลที่จะออกมา เช่น เรามีจุดสี 2 จุด เมื่อขยายจุดสีเป็น 2 เท่า คำถามคือ ช่องว่างที่เกิดขึ้นนั้นจะเติมสีใด เราต้องหาสีที่นำมาแทรกแล้วไม่ก่อให้เกิดเหมือนเม็ดสีเป็นเม็ดสี่เหลี่ยม การประมาณค่าสีตรงช่องว่างจึงเป็นสิ่งที่ต้องกระทำ เป็นต้น

สุดท้ายนี้ขอให้สนุกกับการเขียนโปรแกรมครับ

เอกสารอ้างอิง

1. scipy.optimize.newton
2. scipy.optimize.bisect
3. scipy.optimize.fmin
4. numpy.trapz.

(C) 2020, โดย อ.ดนัย เจษฎาฐิติกุล/อ.จารุต บุศราทิจ
ปรับปรุงเมื่อ 2020-11-10