[EN] ulab EP2 array

From ulab EP 1, we have installed and used ulab for a bit to see how it works. This article discusses the array that can be used to create more variety of 1D and 2D arrays. Along with usage examples, this EP will add more about the different operators that are used with the generated arrays.

array

An array submodule is a module used to create both 1D and 2D array data. The data generated from ulab is either in the form of an ndarray or an array. The format of creating a 1D array is as follows:

object = ulab.array([member₁, member₂, …, member_n], dtype=type)

Creating a 2D array has the following format:

object = ulab.array( [ [member_row1col1, member_row1col2, …, member_row1coln], [member_row2col1, member_row2col2, …, member_row2coln], … , [member_rowmcol1, member_rowmcol2, …, member_rowmcoln] ], dtype=type

ndarray data types support operator marks ==, !=, <, <=, >, >=, +, -, /, *, **, +=, -=, *=, /=, **= and Data prefixes like – and +, for example -a or +a, and support the following functions:

1. len() return ndarray’s number of members
2. abs( ) return absolute value of member in ndarray

The functions of the array submodules that can be called are as follows:

1. object.reshape((numberOfRow,numberOfCol)) for converting the order of the data in the new object’s array to be as defined.
2. newObject=object.transpose() for converting data from rows to columns
3. newObject=object.flatten() for converting an object into a 1-dimensional array
4. (numberOfRow,numberOfCol)=object.shape() For reporting the number of rows and columns of an array object in a tuple form.
5. totalMember=object.size() for returning the total number of members in an object.
6. sizeOfmember=object.itemsize() to find the size of each member in an object.

Example 1

Example code18-2 creates objects a, b and c into 1D arrays, then finds the size of a, the absolute value of a, multiplies a by 3, divides a by 2, compares a and b, compares a and c, and finds the result of summation between a and b, and find the difference between a and c, the result is as shown in Figure 1.

# code18-2
import ulab as np
a = np.array([-1,0,1],dtype=np.float)
b = np.array([1,2,3])
c = np.array([-1,0,1],dtype=np.int8)
print("type of a is {}.".format(type(a)))
print("value of a is {}.".format(a))
print("len() of a is {}.".format(len(a)))
print("abs() of a is {}.".format(abs(a)))
print("value of a*3 is {}.".format(a*3))
print("value of a/2 is {}.".format(a/2))
print("value of b is {}.".format(b))
print("value of c is {}.".format(c))
print("a == [1,2,3] ? {}".format(a==b))
print("a == int([-1,0,1]) ? {}".format(a==c))
print("a+b = {}".format(a+b))
print("a-c = {}".format(a-c))

Example 2

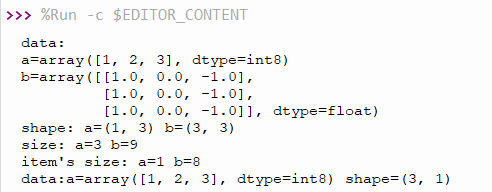
Example code18-3 creates arrays a and b as 1D and 2D, then reports the array size, the size of arrays and try to convert a from the 1D array, 3 members, or (1,3) into (3,1), the result is as shown in Figure 2.

# code18-3
import ulab as np
a = np.array([1,2,3],dtype=np.int8)
b = np.array([[1,0,-1],[1,0,-1],[1,0,-1]],dtype=np.float)
print("data:\na={}\nb={}".format(a,b))
print("shape: a={} b={}".format(a.shape(),b.shape()))
print("size: a={} b={}".format(a.size(),b.size()))
print("item's size: a={} b={}".format(a.itemsize(),b.itemsize()))
a.reshape((3,1))
print("data:a={} shape={}".format(a,a.shape()))

Example 3

Example program 18-4 uses Prewitt’s filter to create a 2D array named Gx, then find Gy which is the transpose of Gx, and try to convert Gx and Gy into 1D arrays. The result is shown in Figure 3.

# code18-4
# Prewitt operator
import ulab as np
Gx = np.array([[1,0,-1],[1,0,-1],[1,0,-1]])
Gy = Gx.transpose()
print("Gx={}\nGy={}".format(Gx,Gy))
print("size: Gx={} Gy={}".format( Gx.size(), Gy.size()))
print("shape: Gx={} Gy={}".format( Gx.shape(), Gy.shape() ))
GxFlat = Gx.flatten()
GyFlat = Gy.flatten()
print("GxFlat={}\nGyFlat={}".format( GxFlat, GyFlat ))
print("size: GxFlat={} GyFlat={}".format( GxFlat.size(), GyFlat.size()))
print("shape: GxFlat={} GyFlat={}".format( GxFlat.shape(), GyFlat.shape()))

Example 4

The example code18-5 is an example of an application for calculating 2D graphics by scaling up rectangle at position (p0,p1,p2,p3) to be 2 times larger by taking the coordinates of the entire 4 points as an array and creating a scaling-up matrix of 2D array and multiplying the matrix p0 with M, p1 with M, p2 with M, and p3 with M (in the matMul function). The result is shown in Figure 4 and an example applied to calculating the size of a rectangle and output to the graphic LCD display is shown in Figure 5 and the video.

#code18-5
import ulab as np
p0 = np.array([-1,1,1],dtype=np.float)
p1 = np.array([1,1,1],dtype=np.float)
p2 = np.array([1,-1,1],dtype=np.float)
p3 = np.array([-1,-1,1],dtype=np.float)

def matMul(p,M):
    x = p[0]*M[0][0]+p[0]*M[1][0]+p[0]*M[2][0]
    y = p[1]*M[0][1]+p[1]*M[1][1]+p[1]*M[2][1]
    z = p[2]*M[0][2]+p[2]*M[1][2]+p[2]*M[2][2]
    return (x,y,z)

def scale(p0,p1,p2,p3,Sx=1.0,Sy=1.0):
    Ms = np.array([[Sx,0.0,0.0],[0.0,Sy,0.0],[0.0,0.0,1.0]],dtype=np.float)
    return (matMul(p0,Ms), matMul(p1,Ms), matMul(p2,Ms), matMul(p3,Ms))

print(scale(p0,p1,p2,p3,2.0,2.0))

Example 5

The example code18-6 is an example of converting data from an array of type ulab.int16 to ulab.float and converting it from ulab.float to ulab.int16. The result is shown in Figure 6.

# code18-6
import ulab as np
a = np.array([1,2,3,4,5], dtype=np.int16)
b = np.array(a,dtype=np.float)
c = np.array(b,dtype=np.int16)
print("a is {}".format(a))
print("b is {}".format(b))
print("c is {}".format(c))

Conclusion

From the article, an array is a sub-module that allows users to create 1D or 2D arrays with a convenient function to report the number of rows/columns, total data size, size of each member, transpose, scaling of arrays, converting multidimensional arrays to 1-dimensional, etc.

The next article will be about vector sub-modules, and hopefully, this article will be more or less helpful. Have fun programming.

(C) 2020, By Jarut Busadathid and Danai Jedsadathitikul
Updated 2021-08-12