[TH] Binary Search Tree data structure programming with Python.

ในบทความก่อนหน้านี้ได้แนะนำการเขียนโปรแกรมเพื่อใช้โครงสร้างข้อมูลแบบคิวไปแล้ว ในบทความนี้จึงแนะนำการเขียนโปรแกรมจัดการโครงสร้างข้อมูล (Data Structure) อีกประเภทหนึ่งซึ่งมีวิธีการจัดเก็บและจัดการที่แตกต่างกันไปอันมีชื่อว่าต้นไม้แบบ BST หรือ Binary Search Tree ดังในภาพที่ 1 ซึ่งเป็นโครงสร้างที่สามารถนำไปประยุกต์เกี่ยวกับการเก็บข้อมูลที่มีคุณลักษณะที่ข้อมูลทางกิ่งด้านซ้ายมีค่าที่น้อยกว่าตัวเอง และกิ่งด้านขวามีค่ามากกว่าต้นเอง หรือทำตรงกันข้ามคือกิ่งซ้ายมีค่ามากกว่า และกิ่งด้านขวามีค่าน้อยกว่า ทำให้การค้นหาข้อมูลในกรณีที่ต้นไม้มีความสมดุลย์ทั้งทางซ้ายและทางขวาบนโครงสร้าง BST ประหยัดเวลาหรือจำนวนครั้งในการค้นหาลงรอบละครึ่งหนึ่งของข้อมูลที่มี เช่น มีข้อมูล 100 ชุด ในรอบแรกถ้าตัวเองยังไม่ใช่ข้อมูลที่กำลังค้นหา จะเหลือทางเลือกให้หาจากกิ่งทางซ้ายหรือขวา ซึ่งการเลือกทำให้ข้อมูลของอีกฝั่งนั้นไม่ถูกพิจารณา หรือตัดทิ้งไปครึ่งหนึ่งโดยประมาณ แต่ถ้าเป็นกรณีที่ Binary Search Tree นั้นขาดความสมดุลย์จะส่งผลให้การค้นหามีความเร็วไม่แตกต่างกับการค้นหาแบบลำดับ (Sequential Search) เท่าใดนัก

ในบทความนี้ใช้ภาษาไพธอนที่ทำงานได้ทั้งบนตัวแปลภาษา Python 3 หรือ MicroPython เพื่อจัดเก็บข้อมูล การเพิ่มข้อมูล การค้นหาข้อมูล เพื่อเป็นตัวอย่างของการนำไปพัฒนาต่อไป

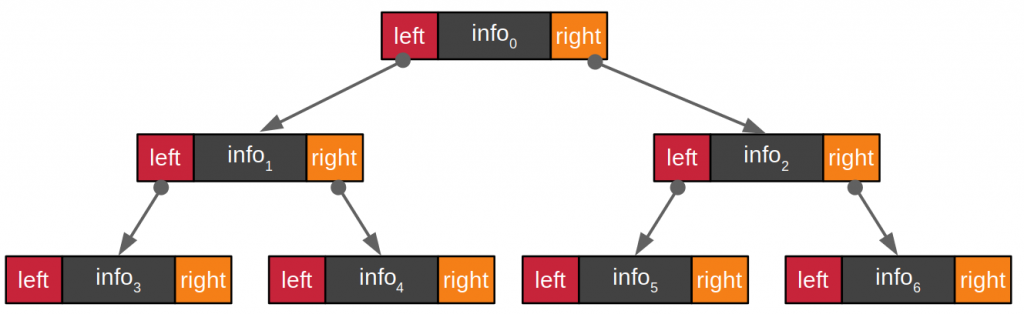
BST : Binary Search Tree — ภาพที่ 1 ตัวอย่าง BST

โครงสร้างข้อมูล BST

โครงสร้างข้อมูลแบบ BST เป็นการเก็บข้อมูลที่มีโครงสร้าง 3 ลักษณะ ดังภาพที่ 1 และ 2 โดยในภาพแรกจะพบว่าข้อมูลที่เก็บในโครงสร้างต้นไม้นั้นประกอบไปด้วย node และใน node นี้เองประกอบไปด้วย 3 ส่วน คือ

left สำหรับเก็บค่าตำแหน่งข้อมูลของโหนดที่อยู่ทางซ้ายมือของโหนดปัจจุบัน
info สำหรับเก็บข้อมูลของโหนดปัจจุบัน
right สำหรับเก็บตำแหน่งของโหนดที่อยู่ทางขวามือ

Binary Search Tree's Node — ภาพที่ 2 โหนดของ BST

โหนดของ BST

จากภาพที่ 2 นำมาเขียนเป็นคลาส BSTNode เพื่อเก็บข้อมูลโหนดของ BST ได้ดังนี้

class BSTNode:
    def __init__(self, info):
        self.left = None
        self.info = info
        self.right = None

ในโค้ดด้านบนจะพบว่า ได้สร้างตัวแปรหรือคุณสมบัติของโหนดไว้ 3 รายการ คือ

left สำหรับเก็บค่าตำแหน่งโหนดทางซ้าย โดยกำหนดค่าเริ่มต้นเป็น None
info สำหรับเก็บค่าข้อมูลที่กำหนดในช่วงของการสร้างต้นไม้ เช่น ต้องการสร้างต้นไม้และให้โหนดแรกเป็น 5 ให้เรียกเป็น
root = BSTNode( 5 )
right สำหรับเก็บค่าตำแหน่งหรือการชี้ไปยังโหนดทางขวา ซึ่งค่าเริ่มต้นของการสร้างโหนดได้กำหนดเป็น None

การเพิ่มโหนด

การเพิ่มโหนดเข้าไปใน BST จะเกิดขึ้นได้ 3 กรณี คือ

ข้อมูลที่เพิ่มนั้นมีอยู่แล้ว
ข้อมูลที่เพิ่มเข้ามานั้นน้อยกว่าโหนดปัจจุบัน
ข้อมูลที่เพิ่มเข้ามีค่ามากกว่าโหนดปัจจุบัน

โดยกรณีที่เป็นข้อมูลมีอยู่แล้วจะรายงานว่าข้อมูลซ้ำ (หรือไม่ต้องรายงานเพื่อเพิ่มความเร็วของการทำงาน)

กรณีที่ข้อมูลอยู่ทางซ้ายจะทำการเรียกซ้ำการเพิ่มโหนดถ้าค่า left ไม่ใช่ None หรือเรียกได้ว่าพบว่าที่โหนดนั้นทางซ้ายมีโหนดลูกอยู่ จึงให้เลื่อนไปทางซ้ายด้วยการเรียกซ้ำ left.insert( ) แต่ถ้าโหนดนั้นมีค่าทางซ้ายเป็น None จะสร้างโหนดใหม่ขึ้นมาด้วยการสั่ง left = BSTNode( ข้อมูล )

เช่นเดียวกันในกรณีที่ข้อมูลที่เพิ่มเข้ามาใหม่นั้นอยู่ทางขวาจะทำการตรวจสอบว่า right เป็น None หรือไม่ ถ้าไม่แสดงว่าทางขวานั้นมีโหนดอื่นอยู่จะทำการเลื่อนและเรียกซ้ำตัวเองโดยเลื่อนไปทางขวาด้วยคำสั่ง right.insert() แต่ถ้าทางขวานั้นว่างจากเพิ่มโหนดใหม่ทางขวาด้วยคำสั่ง right = BSTNode( ข้อมูล )

โค้ดโปรแกรมสำหรับเมธอดหรือฟังก์ชัน insert() เป็นดังนี้

    def insert(self, info):
        if self.info == info:
            print("This information is a duplicate of what already exists.")
            return
        if info < self.info:
            # ย้ายไปทางซ้าย
            if self.left != None:
                self.left.insert( info )
            else:
                self.left = BSTNode( info )
                print("l->{}".format(info))
        # ย้ายไปทางขวา
        if info > self.info:
            if self.right != None:
                self.right.insert( info )
            else:
                self.right = BSTNode( info )
                print("r->{}".format(info))

ตัวอย่างการเรียกใช้งานด้วยคำสั่งต่อไปนี้ได้ผลลัพธ์ดังภาพที่ 3

root = BSTNode( 5 )
root.insert(3)
root.insert(3)
root.insert(7)
root.insert(1)

ภาพที่ 3 ตัวอย่างของการเพิ่มโหนด 5,3,3,7 และ 1

การค้นหา

การค้นหาหรือการท่อง (Traverse) เข้าไปในต้นไม้แบบ BST เพื่อเข้าถึงข้อมูลของแต่ละโหนดนั้นมีด้วยกัน 3 วิธีดังต่อไปนี้

การค้นหาแบบ pre-order

แบบ pre-order มีหลักการทำงานคือทำ VLR ดังนี้

ดึงข้อมูลของตัวเอง (V)
ถ้าไปซ้ายได้ให้ไปทางซ้าย (L)
ถ้าไม่ได้ให้ไปทางขวา (R)

โค้ดโปรแกรมของการทำงาน pre-order เป็นดังนี้

    def preorder(self):
        print(self.info)
        if (self.left is not None):
            self.left.preorder()
        if (self.right is not None):
            self.right.preorder()

การค้นหาแบบ in-order

หลักการทำงานของแบบ in-order แตกต่างออกไป คือ LVR ซึงเป็นดังนี้

ถ้าไปซ้ายได้ให้ไปซ้าย (L)
ดึงข้อมูล (V)
ถ้าไปขวาได้ให้ไปขวา (R)

สามารถเขียนโค้ดของการทำงานแบบ in-order ได้ดังต่อไปนี้

    def inorder(self):
        if (self.left is not None):
            self.left.inorder()
        print(self.info)
        if (self.right is not None):
            self.right.inorder()

การค้นหาแบบ post-order

กรณีของแบบ port-order นั้นทำงานเป็น LRV คือ

ถ้าไปซ้ายได้ให้ไปซ้าย (L)
ถ้าไปขวาได้ให้ไปขวา (R)
ดึงข้อมูล (V)

จากขั้นตอนจะได้ว่า โค้ดของ post-order คือ

    def postorder(self):
        if (self.left is not None):
            self.left.postorder()
        if (self.right is not None):
            self.right.postorder()
        print(self.info)

ตัวอย่างโปรแกรม

ตัวอย่างโปรแกรมสำหรับการเพิ่มโหนดที่มีข้อมูล 5, 3, 7, 1, 0, 2, 4, 6, 9 และ 8 ซึ่งเมื่อทำด้วยมือจะได้ผลลัพธ์ดังภาพที่ 4 และผลลัพธ์ของโปรแกรมตัวอย่างได้ดังภาพที่ 5

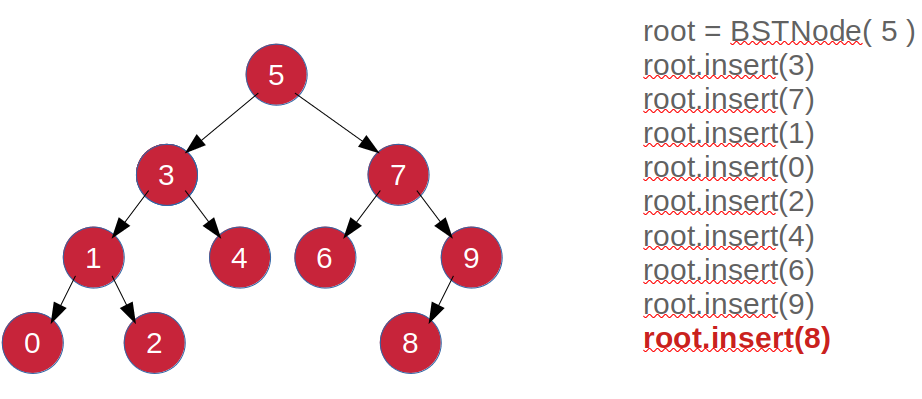
ภาพที่ 4 ตัวอย่างการเพิ่มโหนด 5,3,7,1,0,2,4,6,9 และ 8

# BST
import gc
import sys

gc.enable()
gc.collect()

class BSTNode:
    def __init__(self, info):
        self.left = None
        self.info = info
        self.right = None
       
    def insert(self, info):
        if self.info == info:
            return
        if info < self.info:
            # ย้ายไปทางซ้าย
            if self.left != None:
                self.left.insert( info )
            else:
                self.left = BSTNode( info )
                #print("l->{}".format(info))
        # ย้ายไปทางขวา
        if info > self.info:
            if self.right != None:
                self.right.insert( info )
            else:
                self.right = BSTNode( info )
                
    def preorder(self):
        print(self.info)
        if (self.left is not None):
            self.left.preorder()
        if (self.right is not None):
            self.right.preorder()

    def inorder(self):
        if (self.left is not None):
            self.left.inorder()
        print(self.info)
        if (self.right is not None):
            self.right.inorder()

    def postorder(self):
        if (self.left is not None):
            self.left.postorder()
        if (self.right is not None):
            self.right.postorder()
        print(self.info)
    
root = BSTNode( 5 )
root.insert(3)
root.insert(7)
root.insert(1)
root.insert(0)
root.insert(2)
root.insert(4)
root.insert(6)
root.insert(9)
root.insert(8)
print("Pre-order")
root.preorder()
print("In-order")
root.inorder()
print("Post-order")
root.postorder()

สรุป

จากบทความนี้จะพบว่าการเข้าใจหลักการทำงานของโครงสร้างข้อมูลทำให้สามารถนำมาประยุกต์ใช้กับภาษาไพธอนได้ และถ้าเข้าใจวิธัการเลือกคำสั่งจะทำให้สามารถนำโค้ดเหล่านั้นไปใช้ได้หลากหลายแพล็ตฟอร์ม อย่างตัวอย่างในรอบนี้ผู้เขียนทดสอบในเครื่อง PC ที่เป็น Linux และ macOS และ MicroPython บน ESP32, ESP32-S2 และ ESP32-C3 มีผลการทำงานเหมือนกันทั้ง 5 ระบบ

ข้อดีของ BST ยังคงเป็นกรณีที่เมื่อต้นไม้มีความสมดุลย์จะทำให้การค้นหานั้นรวดเร็วกว่าการค้นหาแบบลำดับมาก ๆ แต่ถ้าเมื่อใดที่ต้นไม้ไม่มีความสมดุลย์ และเสียสมดุลย์ไปทางข้างใดข้างหนึ่งมาก ๆ เช่น ถ้าเพิ่มข้อมูลเป็น 1,2,3,4,5,6,7,8,9 และ 10 จะพบว่าต้นไม้ทั้งหมดเอียงขวา คือ มีแต่โหนดทางขวา เมื่อทำการค้นหาจึงทำงานเหมือนเป็นการหาแบบลำดับ แต่เพิ่มเวลาของการทำงานที่เป็นส่วนของการตรวจสอบโหนดทางซ้าย โหนดทางขวาและการย้ายโหนดเข้าไปจะทำให้ความเร็วของการทำงานนั้นย่ำแย่กว่าการใช้แถวลำดับหรือ Array กับการเก็บข้อมูล 1 ถึง 10 และค้นหาแบบเรียงลำดับ

สุดท้ายนี้ขอให้สนุกกับการเขียนโปรแกรมครับ

แหล่งอ้างอิง

Tutorialspoint: Python – Binary Tree
Wagner Lane: Writing a Binary Search Tree in Python with Examples.

(C) 2020-2021, โดย อ.ดนัย เจษฎาฐิติกุล/อ.จารุต บุศราทิจ
ปรับปรุงเมื่อ 2021-10-30, 2022-01-02