In the previous article, programming to implement queue-based data structures was introduced. In this article, we introduce programming to manage another type of data structure which has different storage and management methods called BST tree or Binary Search Tree, as shown in Figure 1, which is a structure that can be applied to data collection with attributes in which the data in the left branch is less than itself and the right branch is greater than itself or the opposite, i.e. the left branch has a greater value and the right branch is less. It enables searching for data in cases where the tree is balanced on the left and right in the BST structure, saving half the time or number of search times per round of available data, e.g. 100 data sets in the first round if it is not the information you are looking for will be left with a choice to find from the left or right branches which the selection causes the information of the other side is not considered or cut off approximately half. However, if the Binary Search Tree is out of balance, the search speed is not much different from the sequential search.
In this article, we use Python that works on either a Python 3 or MicroPython interpreter to store the data, adding information ,searching for information as an example of further development.
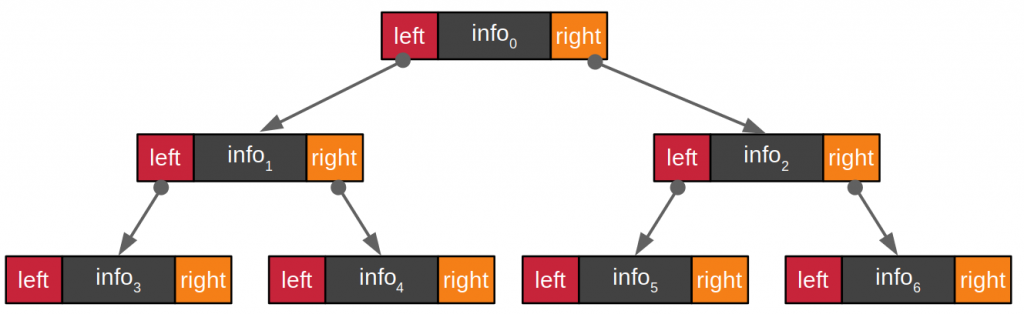
BST data structure
BST data structure is a data storage structure that has 3 characteristics as shown in Figures 1 and 2. In the first Figure, it is found that the data stored in the tree structure consists of nodes and this node consists of 3 parts:
- left to store the address of the node to the left of the current node
- info to store the information of the current node
- right to store the address of the nodes on the right

BST node
From Figure 2, write a BSTNode class to store BST node data as follows:
class BSTNode:
def __init__(self, info):
self.left = None
self.info = info
self.right = NoneIn the code above you will find that three node variables or properties have been created:
- left to store the left node position by default to None
- info for storing data values defined during tree creation, for example, to create a tree and set the first node to be 5, call it
- right to hold the position or point to the right node. The default node creation is set to None.
Adding a Node
Adding a node to BST can happen in 3 cases:
- The added information already exists.
- The added data is less than the current node.
- The added data is greater than the current node.
If the data already exists, it will report that the data is duplicated (or do not report to increase the performance).
If data is left, it will recursively add a node, if the left is not None. So move left with a recursion left.insert( ), but if the node has a left value of None, create a new node with the command left = BSTNode( data ).
Likewise, if the newly added data is on the right, it checks if the right is None or not, if not, there is another node on the right, it will scroll and recursively by scrolling to the right. order right.insert() but if the right is empty then add a new node to the right with right = BSTNode( data )
The program code for the insert() method or function is as follows.
def insert(self, info):
if self.info == info:
print("This information is a duplicate of what already exists.")
return
if info < self.info:
# ย้ายไปทางซ้าย
if self.left != None:
self.left.insert( info )
else:
self.left = BSTNode( info )
print("l->{}".format(info))
# ย้ายไปทางขวา
if info > self.info:
if self.right != None:
self.right.insert( info )
else:
self.right = BSTNode( info )
print("r->{}".format(info))The result is as shown in Figure 3
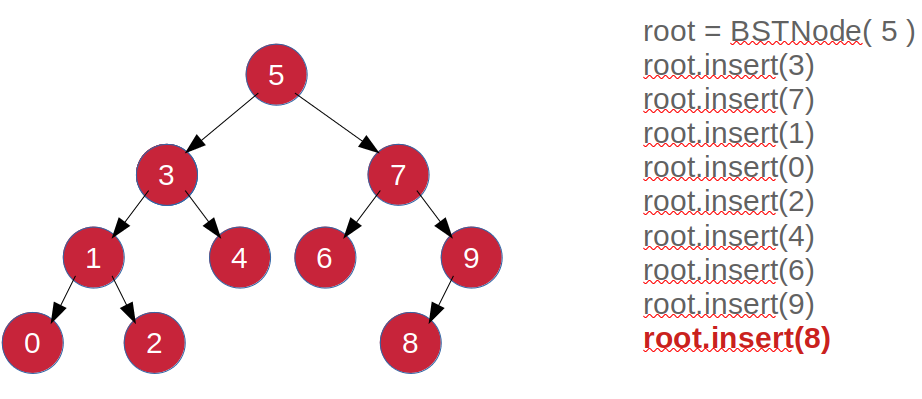
root = BSTNode( 5 )
root.insert(3)
root.insert(3)
root.insert(7)
root.insert(1)
Searching
There are 3 ways to search or traverse into the BST tree to access the data of each node.
pre-order searching
The pre-order model has a working principle of doing VLR as follows:
- Retrieve its data (V)
- If you can go left, go left (L).
- If not, go right (R).
The program code of the pre-order operation is as follows.
def preorder(self):
print(self.info)
if (self.left is not None):
self.left.preorder()
if (self.right is not None):
self.right.preorder()in-order searching
The working principle of in-order is different, LVR is as follows:
- If you can go left, go left (L).
- Retrieve the data (V)
- If you can go right, go right (R)
The in-order operation code can be written as follows:
def inorder(self):
if (self.left is not None):
self.left.inorder()
print(self.info)
if (self.right is not None):
self.right.inorder()post-order searching
In the case of the port-order type that works as an LRV, it is
- If you can go left, go left (L).
- If you can go right, go right (R)
- Retrieves data
From the steps, we can see that the post-order code is
def postorder(self):
if (self.left is not None):
self.left.postorder()
if (self.right is not None):
self.right.postorder()
print(self.info)
Example Code
An example program for adding nodes with data 5, 3, 7, 1, 0, 2, 4, 6, 9 and 8, which when done manually will produce the output as shown in Figure 4. And the output of the sample program is shown in Figure 5.
# BST
import gc
import sys
gc.enable()
gc.collect()
class BSTNode:
def __init__(self, info):
self.left = None
self.info = info
self.right = None
def insert(self, info):
if self.info == info:
return
if info < self.info:
# ย้ายไปทางซ้าย
if self.left != None:
self.left.insert( info )
else:
self.left = BSTNode( info )
#print("l->{}".format(info))
# ย้ายไปทางขวา
if info > self.info:
if self.right != None:
self.right.insert( info )
else:
self.right = BSTNode( info )
def preorder(self):
print(self.info)
if (self.left is not None):
self.left.preorder()
if (self.right is not None):
self.right.preorder()
def inorder(self):
if (self.left is not None):
self.left.inorder()
print(self.info)
if (self.right is not None):
self.right.inorder()
def postorder(self):
if (self.left is not None):
self.left.postorder()
if (self.right is not None):
self.right.postorder()
print(self.info)
root = BSTNode( 5 )
root.insert(3)
root.insert(7)
root.insert(1)
root.insert(0)
root.insert(2)
root.insert(4)
root.insert(6)
root.insert(9)
root.insert(8)
print("Pre-order")
root.preorder()
print("In-order")
root.inorder()
print("Post-order")
root.postorder()

Conclusion
macOS และ MicroPython บน ESP32, ESP32-S2 และ ESP32-C3 มีผลการทำงานเหมือนกันทั้ง 5 ระบบ
From this article, you will find that understanding the working principle of data structures can be applied to Python. If you understand how to select commands, you can apply those codes to a variety of platforms. As an example in this article, we tested on a PC running Linux and macOS, and MicroPython on ESP32, ESP32-S2 and ESP32-C3 had the same performance on all 5 systems.
The advantage of BST is still the case that when the tree is balanced it makes searching much faster than a sequential search. But when the tree is out of balance and loses the balance to one side a lot, for example, if adding data to 1,2,3,4,5,6,7,8,9 and 10 all trees are right-skewed, i.e. only the right node. When searching, it works like a sequential search but increases the time of operation that is part of the left node check, right node and node moving will make the execution speed worse than using an array with 1 to 10 data storage with sequential search.
Finally, have fun with programming.
References
- Tutorialspoint: Python – Binary Tree
- Wagner Lane: Writing a Binary Search Tree in Python with Examples.
(C) 2020-2022, By Jarut Busarathid and Danai Jedsadathitikul
Updated 2022-01-08