[TH] Calculate Regression with MicroPython on esp32-C3.

บทความนี้กล่าวถึงการคำนวณค่าถดถอย (Regression) ด้วยภาษาไพธอนของ MicroPython โดยใช้บอร์ดไมโครคอนโทรลเลอร์ ESP32-C3 พร้อมทั้งแสดงผลด้วยจอแสดงผลกราฟิกแบบ 2 สี (แสดงกับไม่แสดงเม็ดสี) แบบ OLED ดังภาพที่ 1 ซึ่งค่าที่นำมาใช้เป็นตัวอย่างในการใช้งานเป็นค่าที่ได้จากการอ่านอุณหภูมิ

สมการถดถอย

สมการถดถอย หรือ Regression Formula ใช้เพื่อประเมินความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระ โดยแสดงความสัมพันธ์ในรูปแบบของสมการเส้นตรงดังสมการนี้

y = Ax +B

โดย A คือค่าความชัน (slope) ของเส้นตรง และเป็นค่าที่ต้องหาจากข้อมูลที่มีอยู่ เพื่อใช้เป็นค่าความชันที่เป็นตัวแทนของข้อมูล x ที่เป็นตัวแปรอิสระ และตัวแปรตาม y ซึ่งค่า B เป็นเป็นค่าคงที่

การนำวิธีการคำนวณความถดถอยนิยมใช้วิเคราะห์ค่าทางสถิติเพื่อประเมินความสัมพันธ์ระหว่างตัวแปรอิสระแบบหนึ่งตัวขึ้นไป และเป็นตัวแปรที่ขค้นต่อกัน ซึ่งสมการถดถอยมีรูปแบบของสมการดังนี้

Y = a + bX + c

โดยที่

• Y เป็นตัวแปรตาม
• x เป็นตัวแปรอิสระ
• a เป็นจุดตัดบนแกน (intercept)
• b เป็นความลาดชัน (slope)
• c เป็นค่าอื่นๆ ที่เกิดจากความผิดพลาด (error) ในที่นี้กำหนดให้เป็น 0

และจากบทความของ Harsh Katana ในเรื่อง Regression Formula ได้ว่า

a=( (Σy)(Σx²) – (Σx)(Σxy) ) / ( n(Σx²) – (Σx)²)

b= (n (Σxy) – (Σx)(Σy) ) / (n(Σx²) – (Σx)²)

ขั้นตอนของการสร้างตัวแบบทำนายด้วยการใช้สมการถดถอยประกอบด้วย 3 ขั้นตอน คือ

1. เก็บข้อมูลจริง
2. สร้างตัวแบบ
3. ทดสอบตัวแบบ

ในบทความนี้ได้ใช้ข้อมูลจากการเก็บค่าอุณหภูมิใน 1 วัน โดยเก็บทุก 1 ชม. ทำให้มีข้อมูลทั้งสิ้น 24 รายการดังตารางที่ 1

ชั่วโมง	อุณหภูมิ
0	29.5
1	29.2
2	29.0
3	28.9
4	28.6
5	28.8
6	28.5
7	28.3
8	29.0
9	29.6
10	30.8
11	31.8
12	31.7
13	32.1
14	32.5
15	31.6
16	30.5
17	30.5
18	30.2
19	29.6
20	29.5
21	29.2
22	28.1
23	28.9

จากตารางที่ 11 นำมาสร้างตัวแบบด้วยการหาค่าตัว a และ b ได้ค่าดังนี้

x = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]
y = [29.5,29.2,29.0,28.9,28.6,28.8,28.5,28.3,29.0,29.6,30.8,31.8,31.7,32.1,32.5,31.6,30.5,30.5,30.2,29.6,29.5,29.2,28.1,28.9]
n = len(x)
sumX = 0.0
sumY = 0.0
sumX2 = 0.0
sumY2 = 0.0
sumXY = 0.0
for i in range(len(x)):
    sumXY = (sumXY+(x[i]*y[i]))
    sumX2 = (sumX2+(x[i]*x[i]))
    sumY2 = (sumY2+(y[i]*y[i]))
    sumX = (sumX+x[i])
    sumY = (sumY+y[i])
a = ((sumY*sumX2)-(sumX*sumXY))/((n*sumX2)-(sumX*sumX))
b = ((n*sumXY)-(sumX*sumY))/((n*sumX2)-(sumX*sumX))
print("Y = ({})+({}*x)+c".format(a,b))

ส่วนการนำตัวแบบไปใช้ไม่ขอกล่าวถึงในบทความนี้เนื่องจากเป็นการใส่ค่า X เพื่อหา Y จากตัวแปร a และ b ซึ่งด้วยจากตัวอย่างมีข้อมูลเพียง 1 วันของสถานที่หนึ่ง ดังนั้น เมื่อนำไปทำนายของวันถัดไปอาจจะได้ค่าที่ไม่แม่นยำ และด้วยการที่เป็นเพียงสถานที่แห่งหนึ่งซึ่งไม่อาจจะเป็นตัวแทนของทุกพื้นที่ได้ จึงทำนายได้ล่วงหน้าว่า ตัวแบบนี้ไม่ค่อยน่าเชื่อถือ ( 😀 ) แต่นำมาใช้เป็นข้อมูลสำหรับฝึกหัดเขียนโปรแกรมแทนการสุ่มค่า

ตัวอย่างโปรแกรม

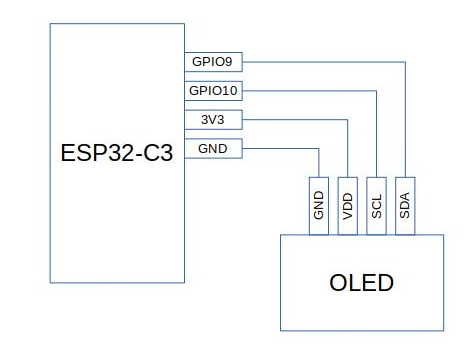
ผังวงจร

ผังวงจรสำหรับการทดลองในครั้งนี้เป็นดังภาพที่ 2

โค้ดโปรแกรม

โปรแกรมสำหรับคำนวณค่า a และ b แล้วนำไปพล็อตกราฟของข้อมูล x, y และกราฟตามค่า a,b เป็นดังนี้

###########################################################
# calculate regression
# jarutex.com
###########################################################
import gc
import time as tm
import machine as mc
from machine import Pin,ADC,I2C
from ssd1306 import SSD1306_I2C

###########################################################
# setting
###########################################################
gc.enable()
gc.collect()

mc.freq(160000000)

pinScl = Pin(10)
pinSda = Pin(9)

i2c = I2C(0,scl=pinScl,sda=pinSda,freq=800000)
oled_addr = const(0x3c)
oled = SSD1306_I2C(128,64,i2c)

x = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]
y = [29.5,29.2,29.0,28.9,28.6,28.8,28.5,28.3,29.0,29.6,30.8,31.8,31.7,32.1,32.5,31.6,30.5,30.5,30.2,29.6,29.5,29.2,28.1,28.9]
n = len(x)
sumX = 0.0
sumY = 0.0
sumX2 = 0.0
sumY2 = 0.0
sumXY = 0.0

###########################################################
# start
###########################################################
oled.poweron()
oled.init_display()
oled.fill(1)
oled.text("JarutEx", 10, 10, 0)
oled.show()

###########################################################
# main program
###########################################################
#
# calculate
#
for i in range(len(x)):
    sumXY = (sumXY+(x[i]*y[i]))
    sumX2 = (sumX2+(x[i]*x[i]))
    sumY2 = (sumY2+(y[i]*y[i]))
    sumX = (sumX+x[i])
    sumY = (sumY+y[i])
a = ((sumY*sumX2)-(sumX*sumXY))/((n*sumX2)-(sumX*sumX))
b = ((n*sumXY)-(sumX*sumY))/((n*sumX2)-(sumX*sumX))
#
# draw axis
#
oled.fill(0)
posx = 0
posy = 0
for i in range(25):
    if ((i % 8)==0):
        oled.text("{}".format(i),8+posx*36,56)
        posx+=1
for posy in range(64):
    oled.pixel(4,posy,1)
for posx in range(128):
    oled.pixel(posx,54,1)
oled.show()
#
# point (x,y)
#
for posx in range(n):
    print(posx*5+8,int(y[posx]))
    oled.text("+",8+posx*5,int(y[posx]))
    #oled.pixel(posx*5+8,int(y[posx]),1)
oled.show()
#
# draw Y = a + bX + c
#
for posx in range(8,124,1):
    posy = a+b*posx
    oled.pixel(posx,int(posy),1)
    
oled.show()
tm.sleep_ms(10000)

###########################################################
# end of program
###########################################################
oled.fill(0)
oled.show()
oled.poweroff()

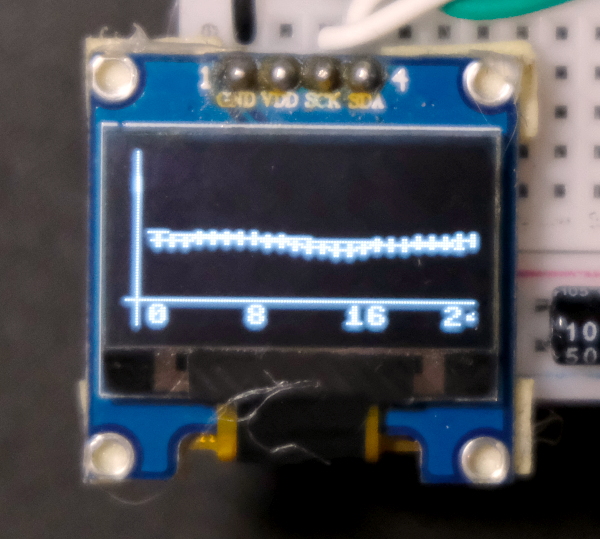
ตัวอย่างผลลัพธ์เป็นดังภาพที่ 3

สรุป

จากบทความนี้จะพบว่า การเขียนโปรแกรมเป็นเพียงเครื่องมือหนึ่งสำหรับควบคุมสมองกลฝังตัวเพื่อให้ทำงานตามที่เราต้องการ ซึ่งการเขียนโปรแกรมจะต้องเข้าใจถึงสิ่งที่ต้องการทำ เช่นในครั้งนี้ต้องการทดลองเรื่องสมการถดถอย ผู้เขียนโปรแกรมต้องเข้าใจวิธีการคำนวณ พร้อมทั้งเข้าใจประโยชน์และการนำไปใช้ และตัวอย่างในบทความนี้เป็นการเริ่มต้นการเขียนโปรแกรมเพื่อสร้างโมเดลการทำนายค่าอุณหภูมิ แต่ด้วยการที่มีข้อมูลปริมาณน้อย (เพียง 1 วัน และ ณ ที่แห่งหนึ่ง) ทำให้โมเดลที่ได้นั้น (ค่า a,b) ไม่ครอบคลุมอย่างที่ควรจะเป็น ดังนั้น ถ้าต้องการนำไปใช้ต่อ ผู้อ่านจะต้องมีข้อมูลจริงที่มากเพียงพอ และเป็นตัวแทนของประชากรข้อมูล เพื่อให้โมเดลนั้นมีความแม่นยำ และ สุดท้ายขอให้สนุกกับการเขียนโปรแกรมครับ

แหล่งอ้างอิง

1. Harsh Katara, Regression Formula, เข้าถึงเมื่อ 2021-10-25

(C) 2020-2021, โดย อ.ดนัย เจษฎาฐิติกุล/อ.จารุต บุศราทิจ
ปรับปรุงเมื่อ 2021-10-25